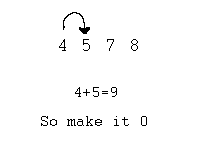
Navasesh

Remainder when divided by 9

    Here is a method for checking your answers after multiplication. But before getting into the method you should know what navasesh means and how to obtain the navasesh of a number.

Navasesh of a number is "the remainder obtained when the number is divided by 9".

For example,

• navasesh of 24 is 6

• navasesh of 63 is 0

• navasesh of  110 is 2

Now, it is easier to calculate the navasesh of smaller numbers by dividing the number by 9. In the case of larger numbers this may be a time consuming process. So here is a method of finding the navasesh of a number without dividing the number.

All you've to do is to sum the digits of the number to a single digit. This single digit is the navasesh of the number.

For example,navasesh of 24 is 2+4=6

            navasesh of 233 is 2+3+3=8

Looks much simpler! Doesn't it? This process can be carried out mentally. Now,there may be occasions while carrying out the addition process , where   the sum equals or exceeds 9. If the sum equals 9, treat it as 0, and continue adding the other digits. If it exceeds 9, then add the individual digits of the sum, and continue adding the rest of the digits.

For example consider finding the navasesh of 4578 mentally.

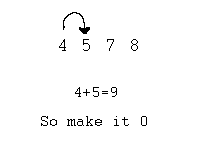
  The sum 4+5=9 (equals 9). So the sum is 0. Continue adding  0 with 7. 0+7=7.

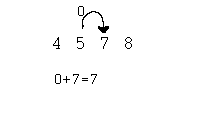
Again when 7+8=15,reduce the sum to 1+5=6.

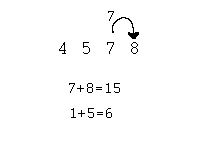
6 is the navasesh of 4578.

For some more examples click here.

Now that you are familiar with finding navasesh of a given number here comes the method of checking your answers after multiplication.

Consider the multiplication of 789 by 67. If you multiply, you'll get the  answer as 52863. We can check this result as follows:

• Find the navaseshs of the two multiplicands.

  Navasesh of 789 is 6 and that of 67 is 4.

•   Find the product of the two navaseshs.

   6 x 4 =24.

• Now find the navasesh of this product.

  Navasesh of 24 is 6.

Let us call this 6 as the product navasesh.

•   Now find the navasesh of your answer.  If it is not equal to the product navasesh then your answer is wrong.

Navasesh of 52863 is 6, which is equal to product navasesh.

Now you think your answer is correct.

Warning:-

It is possible that you arrive at a wrong answer whose Navsesh is that of the actual answer. For example,

the navasesh of 52863 and that of 51963 are equal! You may be fooled and you think the wrong answer is right. But the possibility of this occuring in an actual multiplication is very low. But, at the same time, if the Navaseshs are not equal the method assures you that your answer is definitely wrong!