Pythagorus Theorem

One major development in geometry is the famous Pythagorus theorem, which states that the square of the hypotenuse in a right triangle is the sum of the squares of the other two sides. It is believed that Indian mathematicians provided a proof for this theorem, before Pythagorus himself did ! Let us look at some of the proofs that Indian mathematicians offered.

Bhaskara's proof for the "Pythagorus" theorem.

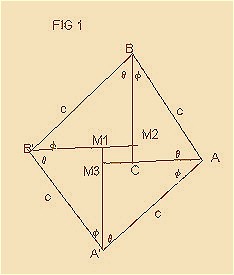
ABC is a right angled triangle. Draw A'M1 || BC and B'M2 perpendicular to BC. We now have four congruent triangles , namely, A'AM3 ,BB'M2 ,B'A'M1 & ABC. Let area of triangle ABC = D. Then sum of the areas of the four triangles = 4D. Now , 4D = 4 (½ * a * b) . Thus,  4D = 2ab. (where a is the length of the side opposite angle A & b is the length of the side opposite angle B.) Since AA'M3 & ABC are congruent , we have  A'M3=AC=b and since B'A'M1 & ABC are congruent we have A'M1=BC=a. Therefore, we have M1M3=A'M1-A'M3 = a - b. Since area(ABB'A')=area(CM2M1M3) + 4D, we obtain c2 = (a-b)2 + 2ab     Hence, c2 = a2 + b2.

The above is a proof offered by Bhaskara for the Pythagorus theorem. Very interesting , isn't it ?