Multiplication                        

     Hi Friends, by this time, you would have appreciated the ease and power of using Indian Mathematics. Previously,you would have learnt some shortcuts for  multiplication, in specific cases (viz. Nikhilam Sutra). Now, we will move on to a more general way of multiplying, that can be applied anywhere. The method is given by Urdhva-TiryagbhyamSutra.

The method is explained with an example.                                     
Let's begin with the multiplication of 4567  with 760.

Reverse one of  the numbers and write it below the other number. In this case, let's reverse 760.

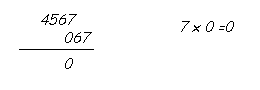
Note the way in which the numbers are written with the last digit ( least significant digit - 7 ) of 4567 and the first digit ( most significant digit - 0 ) of 067 in the same vertical line. Now perform the multiplication of  digits that  fall on the same line. As you do after any multiplication, write the least significant digit of the product in the answer column and keep the remaining digits of the product as carry. The product 7 x 0=0, has only one digit and is written in the answer column. Here, there is no carry.

Shift the reversed number to the left by one digit while keeping the other number stationary. Once this is done, proceed as before.(i.e,) multiply the digits in the same line. But now you would be getting two products (6x0=0 and 6x7=42).

Simply add them like this....

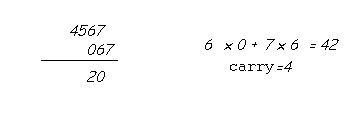
The least significant digit of the sum (2 in 42) forms the next  digit of the result while the remaining digits, ( in this case only one digit - 4 in 42) form the carry to be added during the next stage.

Shift the reversed number  again by one digit to the left. and perform the same process of multiplication and addition. Don't forget to add the result to the carry of the previous stage. This step yields...

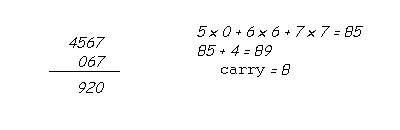
Now we have got the 3 least significant digits of the answer. Just proceed to get the remaining digits. Stop when the digits in the reversed number crosses the number  at the top.

Here's the rest of the steps.

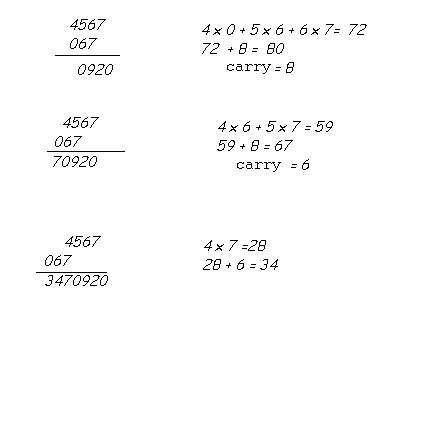
If you shift the reversed number by one more position, none of the digits of the multiplier and the multiplicand will be in the same line. Hence the computation ends. The result of 4567 x 760 is thus 3470920.

Remember this method very well. In future, you'll learn about a process called discrete convolution. The method seen above is nothing but discrete convolutuion, which involves flip (reversing), shift, multiply and add operations.

Continue : Quick recap of the method.